在半导体物理部分我们已经讲过了 pn 结的伏安特性。然而要注意的是,这个关系仅建立在小注入的基础上。作为功率半导体器件, pin 二极管显然在导通状态下要承载大电流,此时小注入的条件已经不再适用,取而代之的是大注入(High Level Injection)条件。本章就来讨论 pin 二极管的正向压降。
1. 霍尔近似
所谓霍尔近似(Hall Approximation)是指:
- 仅考虑 n- 区的复合作用,高掺杂一侧的注入效率为 1
- n- 区近似为本征载流子,即
图 2-1 中的虚线展示了 pin 二极管在大注入条件下 n- 区载流子浓度的分布情况。由于 n- 区既有空穴又有电子,n- 区的电阻很低,这就是所谓的电导调制(Conductivity Modulation)效应。

图 2-1:大注入条件下 pin 二极管的载流子浓度分布
2. 通态压降
通态压降分为三部分,分别是:
- p+n- 结电压
- n- 区漂移电压
- n-n+ 结电压
首先来求
- 连续性方程 →
- 输运方程 →
- 边界条件 →
- n- 区积分 →
根据半导体物理的知识,我们可以分别写出连续性方程和输运方程。在大注入条件下,爱因斯坦关系也成立:
根据输运方程,我们可以把场强表示为:
把方程(2-1)代入输运方程中,再根据爱因斯坦关系式,可以用总电流密度
其中
对于连续性方程,我们也可以做以下简化:
- 稳态载流子 →
- n- 区近似呈现电中性 →
- 大注入条件下载流子的复合机制为 Auger 复合,复合率
由于
再假设 n- 区的电流密度分布是均匀的,那么
公式中的
由于霍尔近似,空穴电流和电子电流分别在
联立方程(2-5)和(2-6)我们可以求出载流子浓度:
由于
在求解
- 方程(2-1)中分子的第二项和扩散系数以及扩散梯度有关,这部分引起的电场叫做 Dember 电场,在 n- 区是可以忽略的
- 考虑正向储存电荷
把方程(2-8)的结果代入到(2-1),再通过积分求出
结电压的求解要简单很多。假设 p+n-
结空穴的浓度为
当然,根据方程(2-7)把载流子浓度带入到(2-2)中求出总电流密度
3. 发射极电流损失
由于 pin 二极管各个区域的掺杂浓度不同,类比晶体管,高掺杂的
p+ 和 n+
区也被称为发射极(Emitter),而低浓度的 n-
区称为基区(Base)。电流从发射极注入到基区时,基区的载流子也会和发射极载流子复合,被称为反注入。而反注入又会导致电流损失。为了更好地描述反注入的损失,我们引入注入效率(Injection
Efficiency)的概念。注入效率被定义为基区中的少子电流和总电流的比值,用
在大注入的电流密度达到 100 - 200
- 高掺杂的区域存在俄歇复合
- 禁带变窄(Bandgap Narrowing)现象
这两点都会加剧注入效率的损失。关于第二点我们不再详细讨论,只给出其原理:高掺杂增加了载流子之间库伦作用的概率,即散射效应。进而导致载流子迁移率降低。随着扩散长度的减少,n- 区的载流子浓度下降。
现在讨论复合的影响。规定中性区和 n- 区的边界为末端(End Region),图 3-1 展示了实际情况下高掺杂的多子和少子浓度。其中上标 * 号表示少子浓度,下标 eff 代表变窄后的禁带实际电离出的载流子浓度。中性区的红线和绿线分别代表电子与空穴的电流密度,n- 区的红线和绿线分别代表电子与空穴的浓度分布。

图 3-1:考虑俄歇复合与禁带变窄的 pin 二极管载流子浓度及电流密度
以左侧的 p+n- 结为例,根据玻尔兹曼分布可以写出:
由此可以得出少子和多子的关系式:
那么基区向 p+ 区反注入的电流密度可以表示为:
这里的
而基区的反注入电流密度总和表示为:
联立方程(2-14)和(2-15),就可以求出考虑俄歇复合的载流子寿命:
而方程(2-9)也应该改写为:
发射区的注入效率可以表示为:
4. 小结
pin 二极管的正向伏安特性曲线如图 4-1 所示。按照注入电流等级从低到高,可以分为四个阶段:
- 复合电流
- 小注入
- 大注入
- 考虑末端高掺杂的大注入
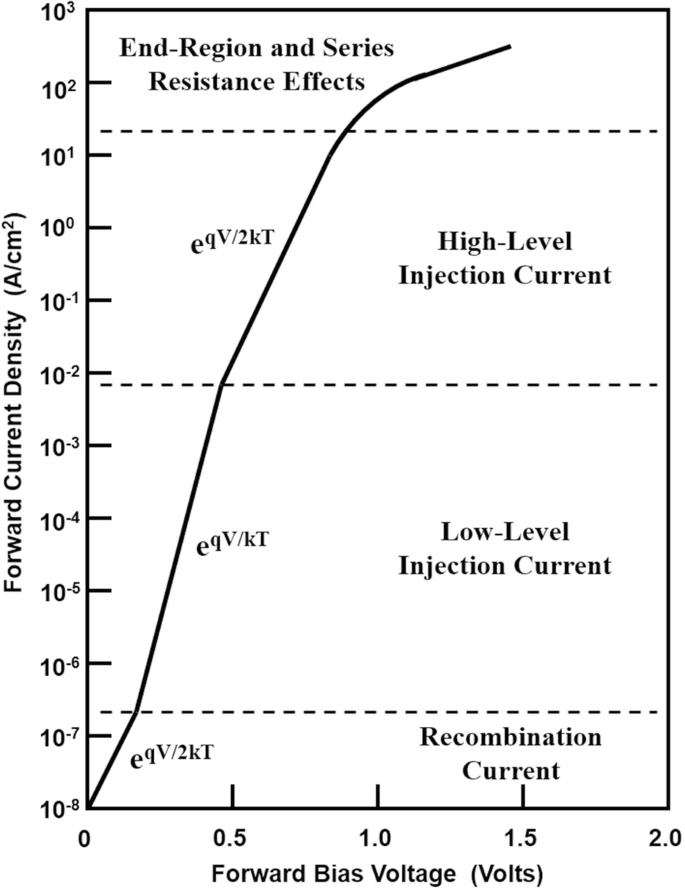
图 4-1:pin 二极管的通态伏安特性曲线
接下来对以上四点进行详细说明。假设施加的外部电压用
- 当
- 当
- 大注入的伏安关系已经在方程(2-11)中给出
- 大注入超过一定范围后,末端的高掺杂导致发射效率进一步降低,电流密度上升变慢