1. 内建电势差
§1.1 形成原因
所谓 pn 结就是分别把掺入受主杂质而形成的 p 区和掺入施主杂质而形成的 n 区用工艺结合到一起。其结构如图 1-1 所示。
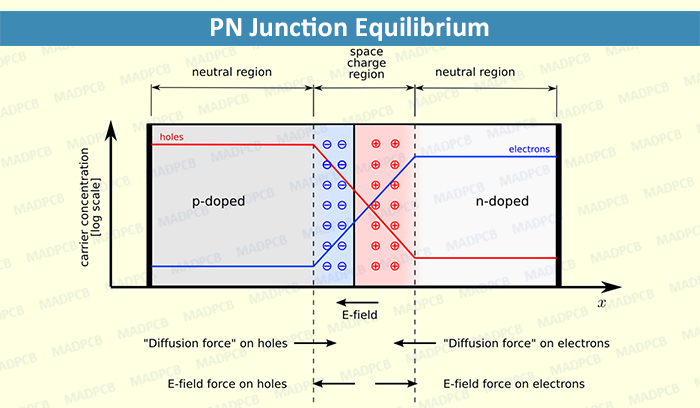
图 1-1:pn 结在热平衡下的载流子分布
由于两边的载流子浓度不同,分别有:
- n 区的多子(即电子)向 p 区扩散
- p 区的多子(即空穴)向 n 区扩散
这种扩散运动的结果就是在 pn 结附近聚集了大量载流子,它们会发生复合,留下不会移动的杂质,从而在 pn 结附近出现一个由 n 指向 p 的电场,被称为内建电场(Build-in E-Field)。这片没有载流子的区域被称为空间电荷区(Space Charge Region),又叫势垒区(Barrier Region)或耗尽层(Depletion Region)。内建电场有对应的内建电压(Build-in Voltage)。因此,只有使 pn 结的正向压降大于内建电压,pn 结才能正向导通。
现在我们关注 pn
结中载流子的浓度情况。电子和空穴的浓度随位置变化的函数分别用蓝色和红色表示。令空穴扩散的长度为
§1.2 基础概念
首先还是要复习一下基础的概念:电压
| 重力势能 | 质量 | 重力加速度 | 高度差 |
|---|---|---|---|
| 电势能 | 电荷量 | 电场场强 | 距离差 |
电势能就是由于电场的存在,检验电荷所具有的能量。那么 ab 两点之间的电势能可以表示为:
可见电势能和电荷量以及位置(距离)有关,为了排除电荷量的影响,我们引入电势,即电势能除以电荷量。而两点的电势差就等于这两点之间的电压。
§1.3 公式推导
所谓零偏是指 pn 结处于热平衡状态。图 1-2 展示了 pn 结的能带图,由三部分组成:
- p 区能带,用蓝色表示
- n 区能带,用橙色表示
- 空间载荷区能带,用绿色表示

图 1-2:热平衡下的 pn 结能带图
通过图 1-2 可以看出:
- 空间载荷区的能带发生了弯曲,在导带和价带,电子和空穴分别从 n 区试图进入到 p 区时遇到势垒
- 热平衡下的费米能级处处相等
- 由于本征费米能级到导带和价带的距离相等,势垒的电势差等于本征费米能级之差
回顾掺杂半导体在热平衡时的载流子浓度,可以写出:
假设半导体内的杂质完全电离,那么
内建电压即为二者的电势差:
其中
注:个人认为,从电势的角度出发进行推导可以和前面掺杂半导体能带的内容联系起来,因此也更容易理解。关于内建电压的推导还有另一种方法,是以输运方程为出发点,空间载荷区的电流密度为零作为条件求解,这也是 BE 课中教授使用的推导方式。这种推导略抽象,因此放在附录中进行展示,在此不再赘述。
2. 电场强度
图 1-3 展示了热平衡条件下 pn 结的电荷密度、场强以及电势差分布。

图 1-3:pn 结在热平衡下的重要物理量:a)电荷量和电荷密度;b)场强;c)电势差
根据 a)图可以分别对 p 区和 n 区的空间电荷区使用泊松方程可得:
对方程(2-1)和(2-2)分别积分,取左右边界的场强为零分别作为积分的上下限,得到 p 区场强分布:
n 区场强分布:
再分别对方程(2-3)和(2-4)积分,令 p 区的左边界电势为零,求出其表达式为:
n 区左边界的电势应该为零,求出 n 区的电势为:
而 n 区右边界的电势应该为内建电压,代入方程(2-6)求得:
方程(2-7)对应图 1-3 的 c)图。同时也解释了图 1-2 中空间载荷区能带弯曲的原因,即电势能和扩散长度的二次方成正比。
3. 扩散长度
pn 结的电场分布如图 1-2 的 b)所示。显然,电场最高的点应该在
依然先把这两个方程写成微分形式然后同时积分可得:
另外,众所周知,电压是电场关于距离的积分,也就是说内建电压是图 1-2 b)的三角形面积:
联立方程(3-1)和(3-2)得到:
那么空间载荷区的长度可以写为:
4. 附录
本章列出内建电压的另一种推导方式。
所谓零偏是指 pn 结处于热平衡状态,由此可得:
假设 p 区和 n
区的杂质完全电离,则有:
首先关注左边,在
求解方程(4-5)的思路是先写成微分的形式,然后两边同时积分,再取对数求得,具体就不再推了,最后的结果是:
同样的思路应用于电子电流密度,求解电子浓度的关系得:
现在我们再来关注右边。我们知道从
也应该符合方程(4-10),由此可得: