1. 载流子浓度

本章将回答 “有多少载流子” 这一核心问题。首先介绍了分析载流子浓度的大前提——热平衡状态。然后分别讨论了本征和掺杂两种情况下，载流子浓度与费米能级的关系以及载流子浓度的近似计算。特别地，温度对电离和本征激发的影响也将被讨论。

§1.1 热平衡

在 Part 1 中，我们介绍了费米分布 和量子态的状态密度函数 。我们假设导带和价带的状态密度函数 和 分别关于禁带中央精准对称。通过分析费米分布的方程，我们知道在绝对零度，即 时有：

• 价带所有量子态都被电子填满
• 导带所有量子态都未被电子占据

然而，根据热力学第三定律，这个绝对零度是永远不可能达到的。再结合热力学第零定律，当我们在讨论载流子浓度(Concentration)时，应该考虑电子的热平衡状态。那么在热平衡状态下载流子浓度计算的基本思路如下：

如果分别用 和 来表示单位体积和单位能量，就可以写出热平衡（Thermodynamic Equilibrium）状态下电子的浓度公式：

对方程（1-1）两边同时积分，体积的下限为 0 ，上限即整条导带的体积；能量的下限是 ，上限则为无穷。代入 Part 0 的公式可得：

其中下标 0 表示电子处于热平衡状态， 是一个参数，代表导带的有效状态密度。

空穴的浓度可以类比电子浓度的计算方式，唯二的不同是：

1. 空穴的费米分布和电子的费米分布关于 对称，表示为
2. 空穴能量积分的上限是 ,下限则为负无穷

那么空穴的热平衡浓度可以表示为：

也是一个参数，代表价带的有效状态密度。

§1.2 本征载流子

所谓本征，就是说半导体晶体内不含杂质和晶格缺陷，用英语 intrinsic 表示。在后面的方程中，下标 i 即代表本征的意思。

由于热能的作用，一个电子从价带跃迁到导带，在导带就会有一个空穴产生，即电子和空穴总是成对存在的，那么（在热平衡条件下的本征半导体中）导带中电子的数量也应该和价带中空穴的数量相等，分别用 和 表示：

本征半导体中载流子的浓度显然符合热平衡定理，故有：

如果把方程（1-2）和（1-3）相乘则有：

方程（1-6）被称为质量作用定律（Law of Mass Action）。

通过方程（1-6）可知，温度和本征载流子浓度成正比，温度越高，本征载流子浓度越高。

如果我们把方程（1-2）和（1-3）分别代入到（1-4）中，就可以求出本征费米能级 的位置：

通过方程（1-7）可知，费米能级的位置和载流子的有效质量有关：

• 若 ，则本征费米能级精确位于禁带中央
• 若 ，则本征费米能级高于禁带中央
• 若 ，则本征费米能级低于禁带中央

§1.3 掺杂

尽管本征载流子的浓度随温度变化明显，但是终归仅占原子密度的万亿分之一，所以本征半导体的导电能力是很弱的。如果我们在其中掺入少量、定量的特定原子来明显改善半导体的电学特性，这些原子被称为杂质（Impurity），这一过程被称为掺杂（Doping），而掺杂后的半导体被称为非本征（extrinsic）半导体。

根据掺杂浓度的多少，非本征半导体的费米能级位置会随之变化：

• 重掺杂时，费米能级位于导带或价带中的称为简明（Degenerate）半导体
• 轻掺杂时，费米能级位于禁带中的非简明（Non-Degenerate）半导体

根据掺杂的类型，非本征半导体分为：

• n 型半导体
  • 常见的替代杂质为 V 族的磷
  • 4 个价电子和硅形成共价键
  • 温度极低时，另一个价电子松散地束缚于磷原子上，被称为施主电子（Donor Atoms）
  • 施主跃迁到导带所需的能量远小于本征原子挣脱共价键所需的能量
  • 一旦施主获得足够的电离能，就可以被电离到导带，留下一个带正电的磷原子。这种能量被称为施主电离能
• p 型半导体
  • 3 个价电子和硅形成共价键
  • 温度极低时，多出的一个空穴松散地束缚于硼原子上，被称为受主电子（Acceptor Atoms）
  • 受主跃迁到价带所需的能量远小于本征原子挣脱共价键所需的能量
  • 一旦受主获得足够的电离能，就可以被电离到价带，留下一个带负电的硼原子。这种能量被称为受主电离能

杂质中的电子 / 空穴从束缚态（Freeze-out）电离所需的电离能（Ionization Energy）远远低于本征激发所需能量。我们把占多数的载流子称为多子（Majority Carries），占少数的载流子称为少子(Minority Carries)。那么可以得出：

• 在 n 型半导体中，电子是多子，空穴是少子
• 在 p 型半导体中，空穴是多子，电子是少子

§1.4 非本征载流子

由于掺杂了其他元素，非本征半导体的费米能级会高于（n 型）或低于（p 型）其本征的费米能级 。我们把方程（1-2）和（1-3）中指数部分的分子项同时加减一个 ，即可求出非本征载流子在热平衡时的浓度：

如果把 和 分别相乘，则仍然符合方程（1-6）。这说明：

• 不管掺杂与否，质量作用定律在热平衡条件下都成立
• 掺杂不改变禁带宽度，只改变费米能级的位置

但需要注意的是，杂质能级和能带中的能级是有区别的：

• 在本征半导体能带中，每个能级可以容纳两个电子
• 在掺杂后，施主能级只能容纳一个电子；受主能级只能容纳一个空穴

鉴于这样的区别，杂质中载流子的分布不能用费米分布描述，故这里特别使用 和 表示电子以及空穴被占据的概率。通过上一节的内容可以总结出杂质中的两种载流子状态：

• 电离态，即被电子和空穴浓度占据的量子态，分别用 和 表示
• 束缚态，即未被占据的电子和空穴浓度，分别用 和 表示（在 Lutz 教授的书中分别用 和 表示）

如果分别用 和 表示施主和受主的掺杂浓度，则有：

根据电中性（Neutron）原理，正负电荷总数相等。那么在 n 型半导体中有：

在 p 型半导体中有：

以 n 型半导体为例，通过方程（1-12）我们可以推测载流子的两个来源：

1. 和本征载流子一样，通过本征激发产生，其多少主要取决于温度
2. 通过施主的电离产生，其多少取决于温度和掺杂浓度

而通过方程（1-10）可知，电离的程度与掺杂浓度和温度有关。图 1-1 描述了 5 中施主电离程度：

0. 绝对零度， ，没有电离产生
1. 低温时只有少量杂质电离。由于本征激发所需能量远大于电离所需能量，低温下 ，根据方程（1-12）可知，
2. 随着温度升高，尽管本征激发产生的电子增加，但相比于电离还是可以忽略不计，所以
3. 温度逐渐升至室温（）， 依然成立。此时施主完全电离，进入饱和状态。热平衡状态下导带中的电子完全由电离产生的电子提供，即 。
4. 温度继续升高，以至于本征激发产生的空穴 不能被忽视，所以
5. 高温下 ，所以

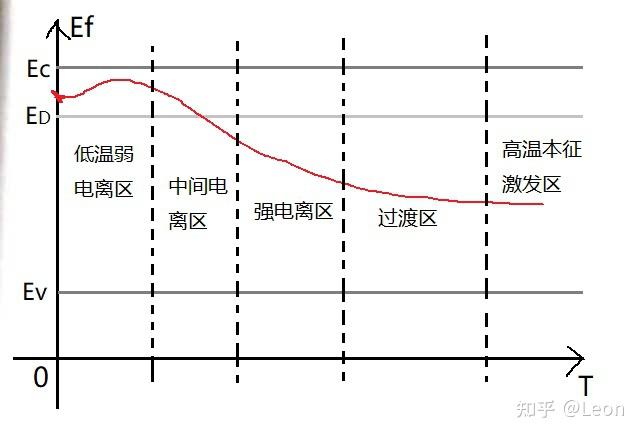
图 1-1：n 型半导体费米能级与温度的关系

p 型半导体可类比 n 型推出。

2. 载流子输运

所谓输运（Transportation）就是指载流子净流动以形成电流的过程。因此，本章将回答“在热平衡状态下，载流子是如何运动，以及为何如此运动” 这一核心问题。首先介绍了载流子的两种基本运动：散射和热运动。然后讨论了载流子在强弱电场下的漂移运动，引出了迁移率这一重要概念。最后，对于非均匀掺杂的半导体还有扩散运动，引出了扩散系数的概念。迁移率和扩散系数的关系也将被提出。

§2.1 散射理论和热运动

首先补充一个固体物理学的概念——散射（Scattering）。理想情况下，载流子由于挣脱了共价键的束缚而自由运动。然而实际情况却并非如此。载流子会受到势场的影响而改变其运动轨迹，这一物理过程被称为散射。在 Part 1 中简单提到过势阱模型。由于晶格的存在导致其内部存在势场，因此晶格相当于是散射中心。晶格还会随温度的升高而加速振动。所以，载流子在经过晶格时会受到晶格散射的影响而改变其运动速度。另外，电离杂质和载流子之间存在库仑作用。由于库仑力引起的碰撞也会影响载流子的速度。综上，我们可以总结出晶体中（主要的）两种散射机制：

• 晶格散射，主要发生在高温
• 电离杂质散射，主要发生在低温

根据有无外部电场影响可以将载流子的运动分为：

• 不受外部电场影响的随机热运动（Thermal Motion）；载流子吸收和发射声子，和晶格不发生能量交换，其速度为 ，满足方程
• 受到外部电场影响的漂移运动（Drift Motion）
  • 弱电场下的（近似）线性漂移运动；载流子从电场获得能量，又以吸收或者发射声子的方式把能量传给晶格，
  • 强电场下的饱和漂移运动；载流子从电场获得过多的能量，以至于其速度

§2.2 漂移运动

先让我们先回顾一下高中物理。空间电荷受到电场力的作用可以表示为：

类比方程（2-1），我们可以推导弱电场下，载流子在电场作用下的运动为：

方程中的 表征载流子的平均漂移速度， 可以理解为粒子受到两次散射的平均碰撞间隔时间。由此可以得出：

这里引入比例系数 µ 以表征漂移速度和弱场强的（近似）线性关系，称为载流子的迁移率(Mobility)。可以看出，迁移率反映了载流子在电场作用下的运动状态。按照温度的高低可以推测出影响迁移率的因素有：

• 低温时电离程度低，电离杂质散射中心随温度升高而减弱，迁移率上升
• 温度继续上升，杂质完全电离，载流子受到电离杂质散射的概率升高，迁移率下降
• 在高温时晶格振动加剧，载流子受到晶格散射的概率就升高，迁移率下降

对于半导体的电阻，我们可以类比金属，用欧姆定律推导。假设有一个长为 dL， 面积为 dA 的半导体立方体。在其两端加上电压 V，就会产生电流 I， 那么根据电流密度、场强和电阻的定义，分别有：

将方程（2-5）和（2-6）分别代入（2-7）即可得到：

称为电导率（Conductivity），电导率的倒数即为电阻率（Resistivity）。方程（2-8）又被称为欧姆定律的微分表达形式。

知道漂移速度后，即可根据电荷流动的分布公式求出电流密度：

总的漂移电流密度为：

可以看出，电阻率受迁移率影响。电阻率随温度变化的关系以及解释如图 2-1 所示。

图 2-1：电阻率和温度达的变化关系

另外，根据方程（2-9），对于单极型器件，如 N 型 MOSFET ，假设杂质全部电离，则可以改写为：

由此可见，电阻率是一个非常重要的概念，它直接决定了 MOSFET 中的 。当然，这个问题以后会详细说明。

以上对漂移速度的讨论，均假设迁移率不受电场影响。然而，随着电场的增强，漂移速度并不会一味地升高。对于硅而言会进入饱和状态（Saturation）；而对于砷化镓而言会在达到峰值后下降，被称为负微分迁移率特性。对于饱和漂移速度的推导不再过多阐释。

§2.3 扩散运动

通量的扩散运动遵循菲克定律（Fick's Law）：

其中 表示空间上的变化浓度（Variable Concentration）， 是梯度算子，表示载流子在多维空间各方向上的浓度变化。

在半导体中载流子也存在这种从高浓度运动到低浓度的运动，称为扩散运动（Diffusion Motion）。为了简化计算，我们现在只考虑浓度在一维方向 x 的变化。那么载流子的扩散电流密度为：

在实际应用中还存在许多非均匀的掺杂。以 n 型半导体为例，在扩散的过程中，带负电的电子流走后剩下带正电的施主杂质粒子。分离的正负电荷会产生一个沿 x 轴正向的电场，以抵抗扩散过程。我们假设满足准电中性条件，则有：

求解 可得：

与 无关， 是场强与电荷的乘积， 对 求导即可求出电场：

现在，我们假设没有外加电场，半导体处于热平衡状态，那么电子的电流密度为零：

由此可以得到：

方程（2-17）被称为爱因斯坦关系式（Einstein Relation）。

需要强调的是，爱因斯坦关系式的使用条件有三种：

• 热平衡（Thermal Equilibrium）
• 非热平衡（Non-thermal Equilibrium）
  • 高电流密度（High Current Densitiy）
  • 高注入水平（High Injection Level）

最后，总电流密度即为漂移和扩散电流之和：